support vector machine

 

Apa itu SVM? Support Vector Machine (SVM) merupakan salah satu metode dalam supervised learning yang biasanya digunakan untuk klasifikasi (seperti Support Vector Classification) dan regresi (Support Vector Regression). Dalam pemodelan klasifikasi, SVM memiliki konsep yang lebih matang dan lebih jelas secara matematis dibandingkan dengan teknik-teknik klasifikasi lainnya. SVM juga dapat mengatasi masalah klasifikasi dan regresi dengan linear maupun non linear.

SVM digunakan untuk mencari hyperplane terbaik dengan memaksimalkan jarak antar kelas. Hyperplane adalah sebuah fungsi yang dapat digunakan untuk pemisah antar kelas. Dalam 2-D fungsi yang digunakan untuk klasifikasi antar kelas disebut sebagai line whereas, fungsi yang digunakan untuk klasifikasi antas kelas dalam 3-D disebut plane similarly, sedangan fungsi yang digunakan untuk klasifikasi di dalam ruang kelas dimensi yang lebih tinggi di sebut hyperplane.

Gambar 1 Hyperplane yang memisahkan dua kelas positif (+1) dan negatif(-1)

Hyperplane yang ditemukan SVM diilustrasikan seperti Gambar 1 posisinya berada ditengah-tengah antara dua kelas, artinya jarak antara hyperplane dengan objek-objek data berbeda dengan kelas yang berdekatan (terluar) yang diberi tanda bulat kosong dan positif. Dalam SVM objek data terluar yang paling dekat dengan hyperplane disebut support vector. Objek yang disebut support vector paling sulit diklasifikasikan dikarenakan posisi yang hampir tumpang tindih (overlap) dengan kelas lain. Mengingat sifatnya yang kritis, hanya support vector inilah yang diperhitungkan untuk menemukan hyperplane yang paling optimal oleh SVM.

Tabel 1 Contoh Data

Dari contoh diatas, didapatkan plot contoh data yang dijelaskan pada Gambar 2.

Gambar 2 Plot Contoh Data

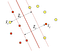
Pada Gambar 2 menjelaskan bahwa terdapat 2 kelas yang terdiri dari -1 ditunjukkan dengan warna biru dan 1 ditunjukkan dengan warna orange. Pada masing-masing titik tersebut digunakan untuk mencari pemisah antara data positif dan data negatif. Penyelesaian sebagai berikut :

Diketahui :

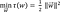
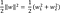
Dengan syarat :

yi(xi . w +b) -1 ≥ 0, i = 1,2,3,….,n

yi(x1.w1 + x2.w2 + b) ≥ 1

sehingga ditemukan persamaan sebagai berikut:

1. (𝑤1 + 𝑤2 + 𝑏 ) ≥ 1 untuk y1 = 1, x1=1, x2=1
2. (−𝑤1 + 𝑤2 − 𝑏 ) ≥ 1 untuk y2 = -1, x1=1, x2=-1
3. (𝑤1 − 𝑤2 − 𝑏 ) ≥ 1 untuk y3 = -1, x1=-1, x2=1
4. (𝑤1 + 𝑤2 − 𝑏 ) ≥ 1 untuk y1 = -1, x1=-1, x2=-1

Berdasarkan persamaan diatas, maka didapatkan nilai dari setiap variabel. Dari persamaan 1 dan 2 didapatkan:

Persamaan 1 dan 3 didapatkan :

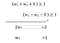
Menjumlahkan persamaan 1 dan 3:

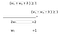
Menjumlahkan persamaan 2 dan 3:

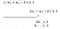
Berdasarkan hasil di atas didapatkan persamaan:

Gambar 3 Menemukan Hyperlane

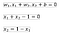
Berdasarkan asumsi diatas berdasarkan asumsi bahwa kedua belah kelas terpisah secara sempurna oleh hyperplane. Dua buah kelas tidak selalu terpisah secara sempurna. Hal tersebut menyebabkan constraint pada persamaan 1 tidak terpenuhi, sehingga optimasi tidak terpenuhi dilakukan. Untuk mengatasi masalah ini, SVM dirumuskan ulang dengan menggunakan teknik soft margin. Soft margin dijelaskan dalam bentuk gambar pada Gambar 4.

Gambar 4 Soft Margin

Persamaan 3.5 dimodifikasi menggunakan soft margin dengan memasukkan variabel slack ξi (ξi > 0) sebagai berikut:

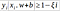
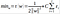
Parameter C dipilih untuk mengontrol trade off antara margin dan error klasifikasi ξ atau nilai kesalahan pada klasifikasi. Parameter C ditentukan dengan mencoba beberapa nilai dan dievaluasi efeknya terhadap akurasi yang dicapai oleh SVM misalnya dengan cara Cross Validation. Nilai C yang besar berarti akan memberikan penalti yang lebih besar terhadap error klasifikasi tersebut.